Curriculum Connections
The mathematics curriculum may vary from one jurisdiction to another, so we want to avoid tying the SNAP math fair to any particular curriculum. However there are certain aspects of a SNAP math fair that are common to every curriculum.
Problem solving
A SNAP math fair is problem based, and a key component of a SNAP math fair is the problem solving that takes place in preparation for the math fair. The focus is on good, challenging, age-appropriate and engaging puzzle problems.
Our teachers are organizing their students into math problem solving teams to dicuss how to solve a math problem and to explore the different ways in which a problem can be solved. As an addititonal challenge we provide more math problem exploration through preparation for a school math fair.Nicole Beaudoin
Assistant Principal from Edmonton, CanadaMath fair puzzles should require a variety of reasoning skills: recognition of patterns, use of a simple mathematical principal. The puzzles may require exploration and conjectures.
There may often be occasions when trial and error will lead a student to a solution even 'though there is a deeper underlying mathematical fact that would have led more efficiently to the solution. In this case, once the student has already solved the puzzle, it is difficult to think of a more compelling motivation to explain the concept, or to show why it is useful.
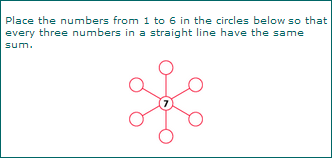
As a particular example, consider the following problem from our puzzle pages, which is considered to be a puzzle suitable for the lower grades:
Problem solving
A SNAP math fair is problem based, and a key component of a SNAP math fair is the problem solving that takes place in preparation for the math fair. The focus is on good, challenging, age-appropriate and engaging puzzle problems.
Our teachers are organizing their students into math problem solving teams to dicuss how to solve a math problem and to explore the different ways in which a problem can be solved. As an addititonal challenge we provide more math problem exploration through preparation for a school math fair.Nicole Beaudoin
Assistant Principal from Edmonton, CanadaMath fair puzzles should require a variety of reasoning skills: recognition of patterns, use of a simple mathematical principal. The puzzles may require exploration and conjectures.
There may often be occasions when trial and error will lead a student to a solution even 'though there is a deeper underlying mathematical fact that would have led more efficiently to the solution. In this case, once the student has already solved the puzzle, it is difficult to think of a more compelling motivation to explain the concept, or to show why it is useful.
As a particular example, consider the following problem from our puzzle pages, which is considered to be a puzzle suitable for the lower grades:
Most children will solve this by trial and error and you should praise their solution even if you didn't expect this approach. In the process of solving it, many will discover that the 7 is unimportant — that they really only have to work with the numbers from 1 to 6, and that they need to partition these six numbers into three pairs each of whose sum is the same.
This will afford them practice in addition. However, they may not recognize that there is another approach: the sum of the numbers from 1 to 6 is 21, and so the sum of the three pairs must be 7, that is, 21 divided by 3. Even if they used a trial and error approach, there is an opportunity to bring in mathematics in a meaningful way when discussing their solution with them.
Communication
Mathematics is not an isolated activity. Students need to learn how to communicate mathematical ideas, questions, and solutions. They should learn how to do this in written form and in conversation, using their own language. When the math fair is presented to the public, the students have an opportunity to practice their communication skills with the visitors.
SNAP math fairs include a hands-on component as an integral part of the investigative strategy and explanation of the problems presented. Most of the time this is done with manipulatives that students build themselves. This helps the students gain ownership of the problem far beyond anything commercially available in the market, and it helps them understand that models, diagrams, and manipulatives can help them communicate.
Their presentations must be attractive, informative, and flexible to accommodate different levels of difficulty.
Other connections
Parts of the above are sometimes stated as separate curriculum objectives. For example, a SNAP math fair is not specifically intended to enhance computational skills. There are, however, certain puzzles that encourage this, but not all of them do. Also, the communication component of the SNAP math fair frequently involves what is commonly thought of as "representation": the students usually have to present the problem in a different setting than it was when they solved it.
In preparing their presentations, students will make connections between mathematics and other disciplines. This helps them understand that mathematics is a useful part of everyday life. One teacher put it this way:
This will afford them practice in addition. However, they may not recognize that there is another approach: the sum of the numbers from 1 to 6 is 21, and so the sum of the three pairs must be 7, that is, 21 divided by 3. Even if they used a trial and error approach, there is an opportunity to bring in mathematics in a meaningful way when discussing their solution with them.
Communication
Mathematics is not an isolated activity. Students need to learn how to communicate mathematical ideas, questions, and solutions. They should learn how to do this in written form and in conversation, using their own language. When the math fair is presented to the public, the students have an opportunity to practice their communication skills with the visitors.
SNAP math fairs include a hands-on component as an integral part of the investigative strategy and explanation of the problems presented. Most of the time this is done with manipulatives that students build themselves. This helps the students gain ownership of the problem far beyond anything commercially available in the market, and it helps them understand that models, diagrams, and manipulatives can help them communicate.
Their presentations must be attractive, informative, and flexible to accommodate different levels of difficulty.
Other connections
Parts of the above are sometimes stated as separate curriculum objectives. For example, a SNAP math fair is not specifically intended to enhance computational skills. There are, however, certain puzzles that encourage this, but not all of them do. Also, the communication component of the SNAP math fair frequently involves what is commonly thought of as "representation": the students usually have to present the problem in a different setting than it was when they solved it.
In preparing their presentations, students will make connections between mathematics and other disciplines. This helps them understand that mathematics is a useful part of everyday life. One teacher put it this way:
"I like to think of the math fair as providing students with an opportunity to do the problem-based mathematics for a particular purpose and to a specific audience, like the language arts. The students understand this line of thinking, and eventually begin to understand that mathematics is no different than any other discipline."
Suhana Kadoura
Teacher from Ottawa, Canada